¿Cómo se ve la media?

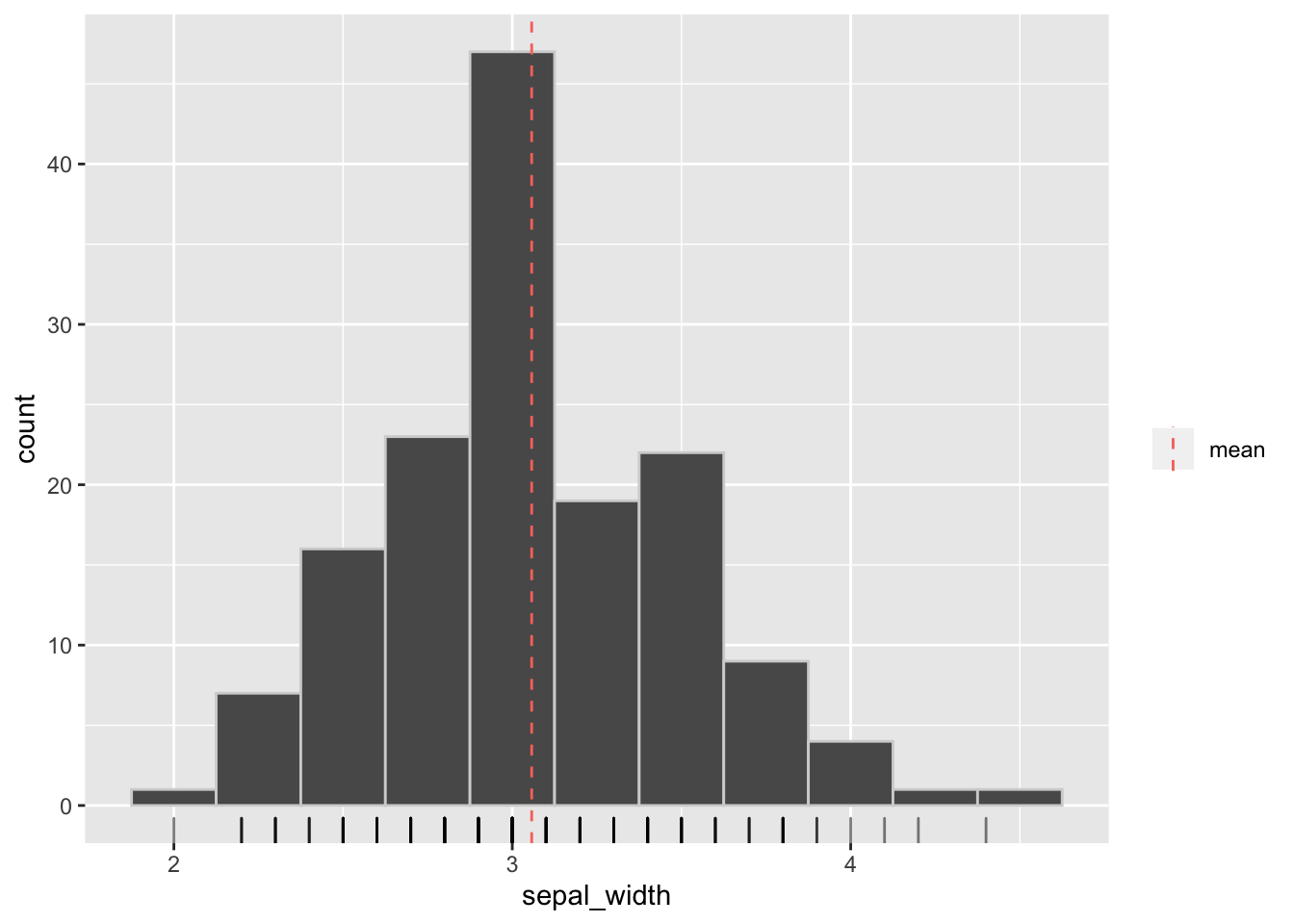
Vamos a graficar la media junto con un histograma. Esto nos ayudará a visualizar dónde está el centro de la distribución.

Para calcular la media en R utilizamos la función mean:

iris %>%
  summarise(
    mean_sepal_width = mean(sepal_width)
  )

## # A tibble: 1 x 1
##   mean_sepal_width
##              <dbl>
## 1             3.06

Propiedades de la media

Dada una muestra de tamaño \(n\), \(x_1, x_2, ..., x_n\), se puede demostrar que la media aritmética, \(\bar{X}\) cumple con las siguientes propiedades:

1. Si a una variable le sumamos una constante o la multiplicamos por una constante, tendremos que sumarle o multiplicarle las mismas constantes a la media. Decimos entonces que la media es un Operador lineal. Formalmente, si aplicamos la transformación lineal \(y_i=ax_i+b\) y calculamos la media, obtendremos el resultado \(\bar{Y}=a\bar{X}+b\).

iris %>% 
  mutate(
    petal_length_plus_one = petal_length + 1,
    petal_length_double = petal_length * 2
  ) %>% 
  summarise(
    petal_length_mean = mean(petal_length),
    petal_length_plus_one_mean = mean(petal_length_plus_one),
    petal_length_double_mean = mean(petal_length_double),
  )

## # A tibble: 1 x 3
##   petal_length_mean petal_length_plus_one_mean petal_length_double_mean
##               <dbl>                      <dbl>                    <dbl>
## 1              3.76                       4.76                     7.52

2. La media de una constante es la constante. Formalmente, si \(x_1 = x_2 = ... = x_n = c\), entonces \(\bar{X} = c\).

iris %>% 
  mutate(
    constant = 10
  ) %>% 
  summarise(
    constant_mean = mean(constant),
  )

## # A tibble: 1 x 1
##   constant_mean
##           <dbl>
## 1            10

3. Si substituímos todos los valores de una variable por su media, el total se mantiene igual. Formalmente:

\[ \sum_{i=1}^{n}x_i = \sum_{i=1}^{n}\bar{X} \]

iris %>% 
  mutate(
    sepal_width_mean = mean(sepal_width)
  ) %>% 
  summarise(
    sepal_width_total = sum(sepal_width),
    sepal_width_mean_total = sum(sepal_width_mean)
  )

## # A tibble: 1 x 2
##   sepal_width_total sepal_width_mean_total
##               <dbl>                  <dbl>
## 1              459.                   459.

Ignorar los NA al calcular la media

A veces los datos no están completos. En R los datos faltantes se representan con NA. Un dato puede falta por ejemplo cuando:

1. La persona no respondió la pregunta porque no sabe o no quiere dar a conocer esta información
2. La pregunta ni siquiera aplica a esa persona, como preguntarle edad del hijo mayor a alguien que no tiene hijos
3. En datos históricos, para una o varias de las unidades de observación no se tiene acceso a los registros para la fecha

Pueden haber otros motivos, pero con estos es suficiente para que te hagas una idea. Cuando hay datos faltantes, la función mean devuelve NA a menos que le digamos que ignore los NA con na.rm = TRUE. Esta es una caracterísica de casi todas las funciones de agregación como mean, sum y var.

Simular datos faltantes

Para simular una situación real en la que hay datos faltantes, puedes imaginarte que en este paso vamos a lanzar una moneda por cada fila; si cae cara, eliminamos el valor de la columna sepal_width, y si cae sello, lo dejamos. Obviamente no vamos a lanzar una moneda real, sino una moneda virtual simulando varios ensayos de Bernoulli, utilizando la función rbinom(n, size, prob).

set.seed(1234567890)

iris_na <- iris %>%
  mutate(
    is_na = rbinom(n(), 1, 0.5),
    sepal_width = if_else(is_na == 1, NA_real_, sepal_width)
  )

iris_na

## # A tibble: 150 x 6
##    sepal_length sepal_width petal_length petal_width species is_na
##           <dbl>       <dbl>        <dbl>       <dbl> <fct>   <int>
##  1          5.1        NA            1.4         0.2 setosa      1
##  2          4.9         3            1.4         0.2 setosa      0
##  3          4.7        NA            1.3         0.2 setosa      1
##  4          4.6        NA            1.5         0.2 setosa      1
##  5          5          NA            1.4         0.2 setosa      1
##  6          5.4        NA            1.7         0.4 setosa      1
##  7          4.6         3.4          1.4         0.3 setosa      0
##  8          5          NA            1.5         0.2 setosa      1
##  9          4.4        NA            1.4         0.2 setosa      1
## 10          4.9        NA            1.5         0.1 setosa      1
## # … with 140 more rows

Mira ahora la diferencia entre usar na.rm = TRUE y no hacerlo.

iris_na %>%
  summarise(
    mean_sepal_width_na_rm = mean(sepal_width, na.rm = TRUE),
    mean_sepal_width = mean(sepal_width)
  )

## # A tibble: 1 x 2
##   mean_sepal_width_na_rm mean_sepal_width
##                    <dbl>            <dbl>
## 1                   3.05               NA

Media truncada

La media es un estadístico no robusto. Esto quiere decir que sensible a los valores atípicos. Intuitivamente, un valor atípico es un valor que no se parece al resto de los valores en un conjunto de datos por ser muy alto o muy bajo. Volviendo al ejemplo de las calificaciones, si tus notas en la mayoría de las asignaturas están entre 11 y 13, pero obtuviste 20 en matemáticas, ese 20 es un valor atípico, y va a halar el promedio hacia arriba, haciendo que tu promedio de una mejor impresión de lo que es tu rendimiento usual. Una manera de solucionar esto es usar una media truncada, en la que eliminamos cierta fracción de los datos más altos y más bajos. En R especificamos esta fracción con el argumento trim.

library(dplyr)
library(janitor)

iris <- as_tibble(iris) %>% clean_names()

iris %>%
  summarise(
    mean_sepal_width_trim = mean(sepal_width, trim = 0.2),
    mean_sepal_width = mean(sepal_width)
  )

## # A tibble: 1 x 2
##   mean_sepal_width_trim mean_sepal_width
##                   <dbl>            <dbl>
## 1                  3.04             3.06

Media ponderada

En algunos casos, hay observaciones que pesan más que otras. También puedes tener una tabla de frecuencias, especificando cada valor y la frecuencia con la que aparece. En estos casos, debemos tomar en cuenta estos pesos o frecuencias al calcular la media. La fórmula de cálculo es la siguiente:

\[ \bar{X} = \frac{\sum_{j=1}^{m}{f_j * x_j}}{\sum_{j=1}^{m}{f_j}} \]

Donde los \(f_j\) son los pesos o frecuencias de los \(x_i\). Para calcular una media ponderada en R utilizamos la función weighted.mean:

df <- tribble(
  ~x, ~f,
  1, 10,
  2, 20,
  3, 30,
  4, 40
)

df %>%
  summarise(
    simple_mean_x = mean(x),
    weighted_mean_x = weighted.mean(x, f)
  )

## # A tibble: 1 x 2
##   simple_mean_x weighted_mean_x
##           <dbl>           <dbl>
## 1           2.5               3

Fíjate cómo la media ponderada es más alta que la media simple porque los valores 3 y 4 tienen más peso que los valores 1 y 2.