Media aritmética

Aunque sea de las primeras cosas que aprendemos en un curso de estadística básica, la media es más compleja de lo que parece a primera vista. ¿Qué hacemos cuando hay valores faltantes? ¿O cómo resolvemos el problema de los valores atípicos? ¿Cómo calculamos la media si tenemos una tabla de frecuencias? Sigue leyendo y resuelvo estas dudas.
El objetivo de este tutorial es que puedas asociar el concepto de Tendencia central con el cálculo de la media y que puedas utilizar python para calcularla en distintos escenarios.
Vamos a descargar iris desde un repositorio público de github. Ya los nombres vienen en un formato legible y que cumple con las características del PEP8
import pandas as pd
iris = pd.read_csv("https://raw.githubusercontent.com/toneloy/data/master/iris.csv")
iris.head()## sepal_length sepal_width petal_length petal_width species
## 0 5.1 3.5 1.4 0.2 setosa
## 1 4.9 3.0 1.4 0.2 setosa
## 2 4.7 3.2 1.3 0.2 setosa
## 3 4.6 3.1 1.5 0.2 setosa
## 4 5.0 3.6 1.4 0.2 setosaDefinición de la media
Cuando estamos en el colegio aprendemos que aunque tenemos una calificación distinta para cada asignatura, nuestro rendimiento global se resume con el promedio o la media aritmética. Es una medida de tendencia central, en el sentido de que su valor tiende a estar en el centro de la distribución de frecuencias. En estadística, la representamos con \(\bar{X}\) y se calcula como:
\[ \bar{X} = \frac{\sum_{i=1}^{n}x_i}{n} \]
Donde las \(x_i\) son los valores que queremos promediar y \(n\) es la cantidad de valores que hay. Es decir, podemos leer la fórmula como la suma de los valores dividida entre la cantidad de valores.
¿Cómo se ve la media?
Vamos a graficar la media junto con un histograma. Esto nos ayudará a visualizar dónde está el centro de la distribución.
## <ggplot: (-9223372036545414056)>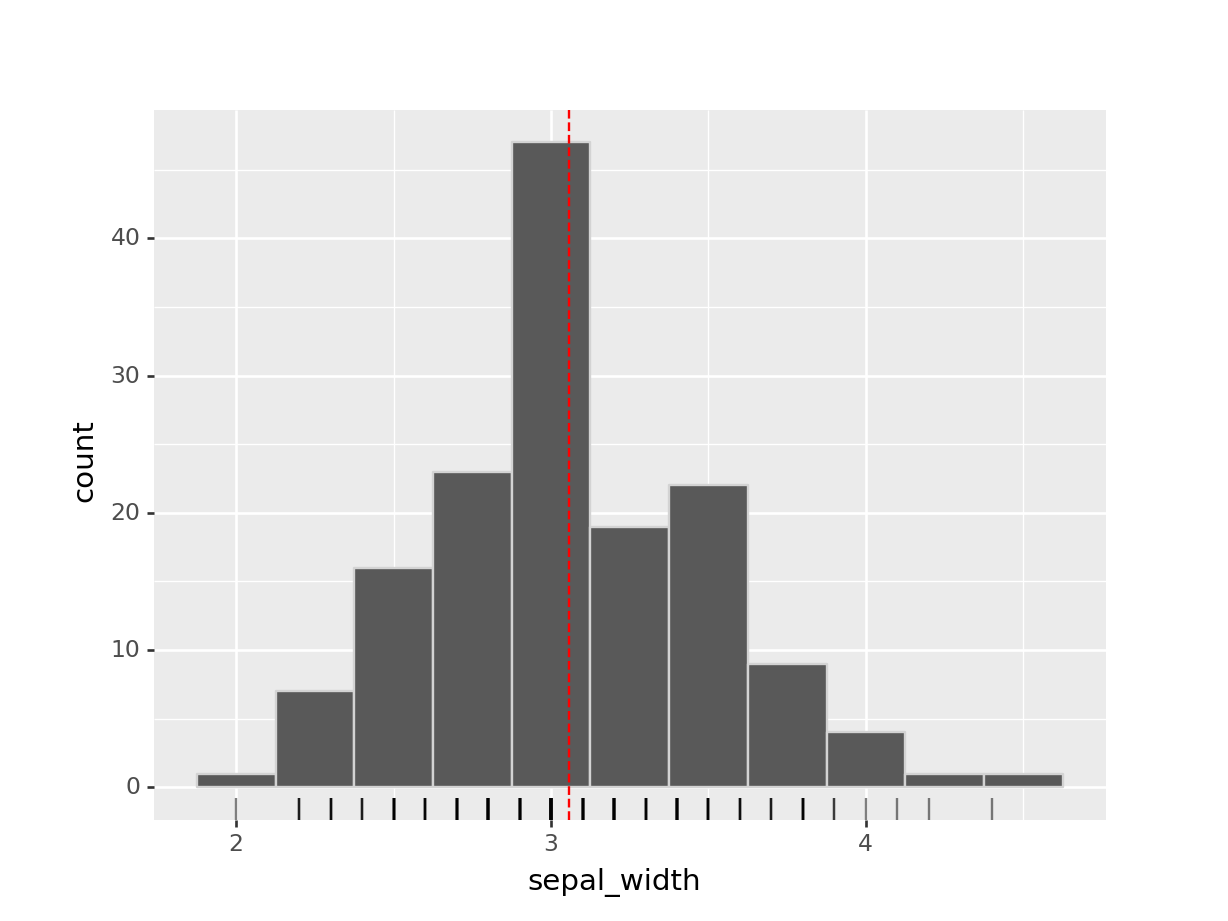
Se puede interpretar la media como el centro de masas de la distribución de frecuencias. Si te imaginas que el eje \(x\) del gráfico es una plataforma, y que las barras del histograma tienen peso, el centro de masa de la plataforma, o el punto donde podrías poner un dedo y que quede equilibrado, estaría aproximadamente donde está la media.
Pregunta
Para calcular la media en python con pandas utilizamos el método mean de la columna:
iris["sepal_width"].mean()## 3.0573333333333337{% notice info %}
Ten en cuenta que a diferencia de la función mean en R, el método .mean de pandas automáticamente elimina los valores faltantes.
{% /notice %}
Hay una manera más similar a lo que haríamos en el tidyverse, utilizando el método agg del DataFrame.
El método agg tiene varias formas de usarse. La que parece más flexible consiste en pasar un diccionario en el que los keys o claves son los nombres de las columnas que queremos agregar y los valores son el nombre del método que queremos utilizar. En el ejemplo siguiente, queremos calcular el método mean de la columna sepal_width.
iris.agg({"sepal_width": "mean"})## sepal_width 3.057333
## dtype: float64Con un pequeño truco podemos conseguir un resultado incluso más parecido al tidyverse. Si primero utilizamos groupby(lambda _: "") para agrupar artificialmente el DataFrame, podemos acceder a una sintaxis más flexible del método agg.
(iris
.groupby(lambda _: "")
.agg(
sepal_width_mean=("sepal_width", "mean"),
sepal_width_sum=("sepal_width", "sum"),
sepal_length_mean=("sepal_length", "mean")))## sepal_width_mean sepal_width_sum sepal_length_mean
## 3.057333 458.6 5.843333Aunque es una sintaxis más avanzada, tiene la ventaja de poder asignar un nombre a cada resultado y podemos agregar la misma columna más de una vez. Además, el resultado siempre es un DataFrame, a diferencia de la sintaxis del ejemplo anterior, que a veces devuelve un objeto Series y otras veces un DataFrame, dependiendo de la estructura de los argumentos.
Propiedades de la media
Dada una muestra de tamaño \(n\), \(x_1, x_2, ..., x_n\), se puede demostrar que la media aritmética, \(\bar{X}\) cumple con las siguientes propiedades:
- Si a una variable le sumamos una constante o la multiplicamos por una constante, tendremos que sumarle o multiplicarle las mismas constantes a la media. Decimos entonces que la media es un Operador lineal. Formalmente, si aplicamos la transformación lineal \(y_i=ax_i+b\) y calculamos la media, obtendremos el resultado \(\bar{Y}=a\bar{X}+b\).
iris["petal_length_plus_one"] = iris["petal_length"] + 1
iris["petal_length_double"] = iris["petal_length"] * 2
iris["petal_length"].mean()## 3.7580000000000005iris["petal_length_plus_one"].mean()## 4.758iris["petal_length_double"].mean()## 7.516000000000001- La media de una constante es la constante. Formalmente, si \(x_1 = x_2 = ... = x_n = c\), entonces \(\bar{X} = c\).
iris["constant"] = 10
iris["constant"].mean()## 10.0- Si substituímos todos los valores de una variable por su media, el total se mantiene igual. Formalmente:
\[ \sum_{i=1}^{n}x_i = \sum_{i=1}^{n}\bar{X} \]
iris["sepal_width_mean"] = iris["sepal_width"].mean()
iris["sepal_width_mean"].sum()## 458.59999999999997iris["sepal_width"].sum()## 458.6Pregunta
- No se puede aplicar la propiedad
- No se puede calcular la media
- Dividir entre una constante es igual a multiplicar por el inverso de la constante
Pregunta
Media truncada
La media es un estadístico no robusto. Esto quiere decir que sensible a los valores atípicos. Intuitivamente, un valor atípico es un valor que no se parece al resto de los valores en un conjunto de datos por ser muy alto o muy bajo. Volviendo al ejemplo de las calificaciones, si tus notas en la mayoría de las asignaturas están entre 11 y 13, pero obtuviste 20 en matemáticas, ese 20 es un valor atípico, y va a halar el promedio hacia arriba, haciendo que tu promedio de una mejor impresión de lo que es tu rendimiento usual. Una manera de solucionar esto es usar una media truncada, en la que eliminamos cierta fracción de los datos más altos y más bajos. En python utilizamos la función scipy.stats.trim_mean.
from scipy.stats import trim_mean
trim_mean(iris["sepal_width"], 0.2)## 3.0399999999999996Media ponderada
En algunos casos, hay observaciones que pesan más que otras. También puedes tener una tabla de frecuencias, especificando cada valor y la frecuencia con la que aparece. En estos casos, debemos tomar en cuenta estos pesos o frecuencias al calcular la media. La fórmula de cálculo es la siguiente:
\[ \bar{X} = \frac{\sum_{j=1}^{m}{f_j * x_j}}{\sum_{j=1}^{m}{f_j}} \]
Donde los \(f_j\) son los pesos o frecuencias de los \(x_i\).
df = pd.DataFrame([
[1, 10],
[2, 20],
[3, 30],
[4, 40]
], columns=["x", "f"])
(df["x"] * df["f"]).sum() / df["f"].sum()## 3.0Fíjate cómo la media ponderada es más alta que la media simple porque los valores 3 y 4 tienen más peso que los valores 1 y 2.